Rozrywki matematyczne
Matematyka zawiera w sobie nie tylko prawdę, ale i najwyższe piękno – piękno chłodne i surowe, podobne do piękna rzeźby.
{Bertrand Russell, 1872-1970}
Matematyka jest piękną dziedziną nauki. Nie ma w niej miejsca na ideologię, jak np. w naukach humanistycznych i społecznych. Wyniki i sukces można osiągnąć dzięki wysiłkowi intelektualnemu — rzetelnej wiedzy, logicznemu myśleniu i niekonwencjonalnej wyobraźni.
Zajmowanie się matematyką nie musi być tylko pracą, może być też przygodą intelektualną, ale i formą rozrywki związanej z gimnastyką umysłową - łamigłówkami. Jednym z przedmiotów matematyki rekreacyjnej są kwadraty magiczne, których historia sięga starożytności.
Kwadrat magiczny
Kwadrat liczbowy to tablica zbudowana z takiej samej, większej od 2, liczby wierszy i kolumn, której komórki wypełnione są liczbami. Kwadrat magiczny n x n to kwadrat liczbowy zawierający niepowtarzające się dodatnie liczby naturalne, rozmieszczone w specjalny sposób, dzięki czemu posiada on pewne "niezwykłe" własności. Jego podstawową własnością jest to, że suma liczb w każdym wierszu, w każdej kolumnie i na głównych przekątnych Główne przekątne kwadratu tworzą elementy położone na przekątnej łączącej lewy górny róg z prawym dolnym rogiem oraz na przekątnej łączącej lewy dolny róg z prawym górnym rogiem. jest taka sama → suma magiczna M2. Istnieją też inne, dodatkowe osobliwości kwadratów magicznych. O niektórych będzie mowa poniżej. Kwadrat, w którym sumy liczb na przekątnych różnią się od sumy liczb w wierszach i kolumnach, nazywa się półmagicznym. Istnieją też "inaczej ułomne" kwadraty liczbowe. Do nich należy m.in. kwadrat 6 x 6, będący składnikiem przedstawionego poniżej magicznego kwadratu 10 x 10.
Wybrane własności kwadratów magicznych
Ciągi liczbowe
Podstawową własnością kwadratów magicznych jest to, że tworzą je niepowtarzające się liczby naturalne. Liczby te tworzą zbiór, którego elementy można uszeregować w ciągi liczbowe. Ciąg liczbowy, w którym każdy wyraz jest sumą wyrazu bezpośrednio go poprzedzającego oraz ustalonej liczby zwanej różnicą ciągu nazywamy ciągiem arytmetycznym (postępem arytmetycznym). Zgodnie z tą definicją dla dwóch kolejnych wyrazów ciągu można napisać:
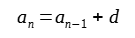 (1)
(1)
gdzie:
an - n-ty wyraz ciągu,
an-1 - bezpośredni poprzednik n-tego wyrazu ciągu,
d - różnica ciągu.
Sumę kolejnych n wyrazów ciągu arytmetycznego można obliczyć ze wzoru:
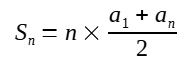 (2)
(2)
gdzie:
n - liczba sumowanych wyrazów ciągu,
a1 - początkowy wyraz ciągu,
an - końcowy wyraz ciągu.
Przykłady:
1. Suma ciągu arytmetycznego o różnicy 1: [1, 2, 3, 4, 5, 6, 7] → 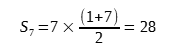 .
.
2. Suma ciągu arytmetycznego o różnicy 3: [7, 10, 13, 16, 19] → 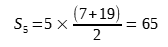 .
.
Jeżeli każdy z wyrazów ciągu pomnożymy przez tę samą liczbę k, to jego suma zwiększy się k-krotnie, a gdy do każdego z nwyrazów ciągu dodamy taką samą liczbę k, to jego suma zwiększy się o n · k.
Przykłady:
3. Jeżeli wyrazy powyższego ciągu 1 pomnożymy teraz przez 5, to otrzymamy nowy ciąg o różnicy 1: [5, 10, 15, 20, 25, 30, 35] → 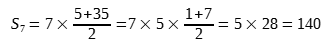 .
.
4. Jeżeli do każdego wyrazu powyższego ciągu 2 dodamy teraz 3, to otrzymamy nowy ciąg o różnicy 3: [10, 13, 16, 19, 22] → 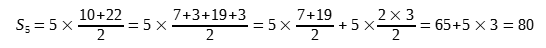 .
.
Jeżeli ciąg arytmetyczny zawiera nieparzystą liczbę wyrazów, to połowa sumy jego dwóch wyrazów oddalonych równo od jego końców równa się wyrazowi środkowemu. Położenie wyrazu środkowego można wyznaczyć z prostego wzoru:
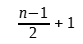 (3)
(3)
gdzie:
n - nieparzysta liczba wyrazów ciągu.
Przykład:
5. Dla ciągu arytmetycznego [a1, a2, a3, a4, a5, a6, a7] = [30, 31, 32, 33, 34, 35, 36] mamy:
— liczba wyrazów ciągu n = 7,
— pozycja wyrazu środkowego: (n - 1)/2 + 1 = (7 - 1)/2 + 1 = 4,
— wartość wyrazu środkowego: 33.
→ a1 + a7 = a2 + a6 = a3 + a5 = 33.
Ta własność ciągów arytmetycznych o nieparzystej liczbie wyrazów ułatwia kontruowanie magicznych kwadratów o nieparzystej liczbie wierszy i kolumn.
Suma magiczna
Powyższe własności ciągów arytmetycznych znajdują zastosowanie w kwadratach magicznych, m.in. do tworzenia ich i obliczania sum magicznych. Należy tutaj wspomnieć, że niektórzy uznają za kwadrat magiczny tylko te kwadraty liczbowe, które są zbudowane z ciągów arytmetycznych o różnicy 1, zaczynających się od 1. Z punktu widzenia funkcji rozrywkowej kwadratów magicznych takie ograniczenie nie jest uzasadnione.
Liczby tworzące kwadraty magiczne mogą stanowić jeden ciąg arytmetyczny lub składać się z kilku ciągów. W pierwszym przypadku sumę magiczną można szybko znaleźć, dzieląc sumę ciągu arytmetycznego przez liczbę wierszy/kolumn kwadratu. Sumę ciągu oblicza się za pomocą wzoru (2), podstawiając za pierwszy wyraz ciągu najmniejszą liczbę wpisaną do kwadratu, a za ostatni - liczbę największą oraz za n - liczbę pól kwadratu. W drugim przypadku sumę magiczną można obliczyć analogicznie, sumując sumy poszczególnych arytmetycznych ciągów składowych.
Przykład:
6. W kwadracie magicznym 4 x 4 ze zbiorem liczb [1,2,3,4,5,6,7,8,29,30,31,32,33,34,35,36], można wyróżnić dwa składowe ciągi arytmetyczne: [1,2,3,4,5,6,7,8] i [29,30,31,32,33,34,35,36]. W tym przypadku suma magiczna jest sumą dwóch
sum wyrazów każdego ciągu składowego, podzieloną przez stopień macierzy, tj. (36 + 260)/4 = 296/4 = 74.
7. W kwadracie magicznym 3 x 3 ze zbiorem liczb [1,7,13,31,37,43,61,67,73], można wyodrębnić trzy składowe ciągi arytmetyczne: [1,7,13], [31,37,43] i [61,67,73]. W tym przypadku suma magiczna jest sumą trzech sum
wyrazów każdego ciągu składowego, podzieloną przez stopień macierzy, tj. (21 + 111 + 201)/3 = 333/3 = 111.
Stosując konsekwentnie wzór (1), otrzymujemy zależność łączącą n-ty wyraz z pierwszym wyrazem ciągu:
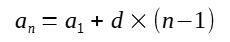 (4)
(4)
Po podstawieniu zależności (4) do wzoru (2) oraz przystosowaniu oznaczeń do specyfiki magicznego kwadratu mamy:
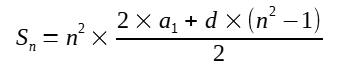 (5)
(5)
gdzie:
n - stopień (liczba wierszy/kolumn) magicznego kwadratu,
n2 - liczba sumowanych wyrazów ciągu kwadratu,
a1 - początkowy wyraz ciągu,
d - różnica ciągu.
Po podzieleniu sumy Sn przez stopień n kwadratu otrzymujemy wzór na jego sumę magiczną, a po podstawieniu w nim 1 za a1 i d dostajemy wzór na minimalną sumę magiczną, zwaną stała magiczną kwadratu stopnia n:
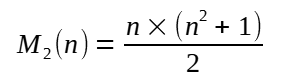 (6)
(6)
Poniżej lista wartości stałej magicznej dla kwadratów stopnia 3-10.
- M2(3) = 15,
- M2(4) = 34,
- M2(5) = 65,
- M2(6) = 111,
- M2(7) = 175,
- M2(8) = 260,
- M2(9) = 369,
- M2(10) = 505.
Znajomość tego parametru magicznych kwadratów ułatwia ich tworzenie.
Jeżeli liczby jakiegoś kwadratu magicznego tworzą ciąg arytmetyczny, którego wyraz początkowy nie jest 1, to oznacza, że jego suma nie jest równa stałej magicznej. Najprostszym sposobem przekształcenia danego kwadratu do postaci, którego suma magiczna ma wartość stałej magicznej jest zapisanie wyrazów ciągu, korzystając z operacji dodawania lub mnożenia tak, aby wyodrębnić podciąg zaczynający się od cyfry 1.
Przykład:
8. Liczby kwadratu magicznego 8 x 8 tworzą ciąg arytmetyczny złożony z 81 wyrazów, zaczynający się od 19. Suma tego ciągu wynosi 3232, a suma magiczna kwadratu - 3232/8 = 404. Aby otrzymać
nowy ciąg zaczynający się od 1 należy jego każdy wyraz pomniejszyć o 18. Suma tego nowego ciągu wynosi 2080, a odpowiadająca mu suma magiczna kwadratu, równa stałej magicznej, - 2080/8 = 260.
Kwadrat magiczny 3 x 3
Najmniejszym nietrywialnym kwadratem magicznym jest kwadrat 3 x 3. Poniżej widok kwadratu utworzonego z cyfr od 1 do 9, którego suma magiczna, a zarazem stała magiczna, jest równa potrojonej cyfrze na środkowym polu, tj. 3 · 5 = 15. Jego "magiczność" i wartość sumy magicznej nie ulega przy zamianie miejscami skrajnych wierszy i kolumn, przestawianiu wierszy i kolumn, ani przy obrocie kwadratu wokół jego środkowego pola - tu z cyfrą 5. Inną cechą tego kwadratu jest to, że sumy liczb w czterech komórkach narożnych oraz środkowych są zawsze równe czterokrotności liczby na środkowym polu.
Te właściwości kwadratu można sprawdzić klikając na jego polach i podając odpowiednie nowe cyfry.
| 2 | 7 | 6 | ||
| 9 | 5 | 1 | ||
| 4 | 3 | 8 | ||
Po obróceniu powyższego kwadratu o 90o (w prawo) otrzymuje się kwadrat odpowiadający chińskiemu kwadratowi Luoshu:
Kwadrat magiczny 4 x 4
Ponższy kwadrat znajduje się na miedziorycie Albrechta Dürera "Melancholia" z 1514 roku:

Tworzą go liczby od 1 do 16. Jego suma magiczna wynosi 34. Posiada on jeszcze inną, przedstawioną dalej, ciekawą własność.
| 16 | 3 | 2 | 13 | ||
| 5 | 10 | 11 | 8 | ||
| 9 | 6 | 7 | 12 | ||
| 4 | 15 | 14 | 1 | ||
| c11 | c12 | c13 | c14 |
| c21 | c22 | c23 | c24 |
| c31 | c32 | c33 | c34 |
| c41 | c42 | c43 | c44 |
Sumy liczb w następujących parach komórek równe są połowie sumy magicznej, w powyższym przypadku 17. Aby zobaczyć położenie tych par, kliknij na odpowiedniej linijce poniższej listy.
Spróbuj, posługując się powyższym schematem, uzupełnić poniższy kwadrat, którego suma magiczna wynosi 74. Klikaj na pustych polach kwadratu i podawaj nowe liczby. Poniższą planszę można wykorzystać też do tworzenia własnych kwadratów magicznych 4 x 4.
| 35 | 34 | ||||
| 32 | 29 | ||||
| 30 | 31 | 5 | |||
| 33 | 36 | ||||
Aby zobaczyć rozwiązanie zadania kliknij → 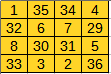
Kwadrat magiczny 5 x 5
Tworzą go liczby od 1 do 25. Jego suma magiczna wynosi 65.
| 23 | 6 | 19 | 2 | 15 | ||
| 4 | 12 | 25 | 8 | 16 | ||
| 10 | 18 | 1 | 14 | 22 | ||
| 11 | 24 | 7 | 20 | 3 | ||
| 17 | 5 | 13 | 21 | 9 | ||
| c11 | c12 | c13 | c14 | c15 |
| c21 | c22 | c23 | c24 | c25 |
| c31 | c32 | c33 | c34 | c35 |
| c41 | c42 | c43 | c44 | c45 |
| c51 | c52 | c53 | c54 | c55 |
Ze wzrostem rzędu kwadratu, zwiększa się liczba jego elementów. Dlatego warto analizować jego budowę, aby tym łatwiej tworzyć nowe kwadraty. Powyższy kwadrat, oprócz klasycznych własności magicznego kwadratu, ma jeszcze następujące cechy:
1. Sumy liczb w następujących czterech komórkach równe są sumie magicznej pomniejszonej o liczbę środkową kwadratu, w powyższym przypadku 65 - 1 = 64. Aby zobaczyć położenie tych czwórek, kliknij na odpowiedniej linijce poniższej listy.
2. Sumy liczb w następujących parach komórek równe są połowie sumy magicznej pomniejszonej o liczbę środkową kwadratu, w powyższym przypadku (65 - 1)/2 = 32. W środku kwadratu znajduje się najmniejsza liczba. Aby zobaczyć położenie tych par, kliknij na odpowiedniej linijce poniższej listy.
Spróbuj, posługując się powyższym schematami, uzupełnić poniższy kwadrat. Zawiera liczby od 6 do 30 a jego suma magiczna wynosi 90. Klikaj na pustych polach kwadratu i podawaj nowe liczby. Poniższą planszę można wykorzystać też do tworzenia własnych kwadratów magicznych 5 x 5.
| 11 | 24 | 7 | ||||
| 9 | 30 | 21 | ||||
| 23 | 19 | 27 | ||||
| 16 | 29 | 25 | ||||
| 22 | 18 | 14 | ||||
Aby zobaczyć rozwiązanie zadania kliknij → 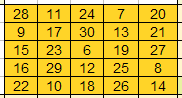
Przykłady kwadratów magicznych większych niż 5 x 5
Kwadrat magiczny 6 x 6
Poniższy kwadrat zawiera liczby od 1 do 36 a jego suma magiczna wynosi 111.
| 1 | 35 | 23 | 14 | 34 | 4 | ||
| 32 | 7 | 15 | 22 | 6 | 29 | ||
| 28 | 10 | 19 | 18 | 25 | 11 | ||
| 9 | 27 | 20 | 17 | 12 | 26 | ||
| 8 | 30 | 21 | 16 | 31 | 5 | ||
| 33 | 2 | 13 | 24 | 3 | 36 | ||
Poniższy kwadrat 6 x 6 zawiera liczby od 33 do 68. Jego suma magiczna wynosi 303. Spróbuj uzupełnić go, klikając na jego pustych polach i podając nowe liczby. Poniższą planszę można wykorzystać też do tworzenia
własnych kwadratów magicznych 6 x 6.
Wskazówka: Porównaj zakresy liczbowe oraz sumy magiczne tego kwadratu i poprzedniego. Zauważ, że 303 -111 = 192 = 6 · 32.
| 68 | 56 | 45 | 34 | ||||
| 63 | 53 | 62 | 40 | ||||
| 58 | 44 | 49 | 52 | 59 | 41 | ||
| 57 | 50 | 51 | 60 | ||||
| 61 | 54 | 47 | 64 | ||||
| 36 | 66 | 55 | 67 | ||||
Aby zobaczyć rozwiązanie zadania kliknij → 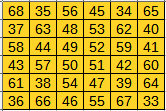
Kwadrat magiczny 7 x 7
Poniższy kwadrat zawiera liczby od 9 do 57 a jego suma magiczna wynosi 231.
| 38 | 47 | 56 | 9 | 18 | 27 | 36 | ||
| 46 | 55 | 15 | 17 | 26 | 35 | 37 | ||
| 54 | 14 | 16 | 25 | 34 | 43 | 45 | ||
| 13 | 22 | 24 | 33 | 42 | 44 | 53 | ||
| 21 | 23 | 32 | 41 | 50 | 52 | 12 | ||
| 29 | 31 | 40 | 49 | 51 | 11 | 20 | ||
| 30 | 39 | 48 | 57 | 10 | 19 | 28 | ||
Kwadrat magiczny 8 x 8
Poniższy kwadrat zawiera liczby od 19 do 82 a jego suma magiczna wynosi 404.
| 26 | 76 | 77 | 23 | 22 | 80 | 81 | 19 | ||
| 67 | 33 | 32 | 70 | 71 | 29 | 28 | 74 | ||
| 59 | 41 | 37 | 63 | 62 | 40 | 36 | 66 | ||
| 50 | 52 | 56 | 46 | 47 | 53 | 57 | 43 | ||
| 58 | 44 | 48 | 54 | 55 | 45 | 49 | 51 | ||
| 35 | 60 | 61 | 39 | 38 | 64 | 65 | 42 | ||
| 27 | 73 | 69 | 31 | 30 | 72 | 68 | 34 | ||
| 82 | 25 | 24 | 78 | 79 | 21 | 20 | 75 | ||
Kwadrat magiczny 9 x 9
Poniższy kwadrat zawiera liczby od 1 do 81 a jego suma magiczna wynosi 369.
| 37 | 48 | 59 | 70 | 81 | 2 | 13 | 24 | 35 | ||
| 36 | 38 | 49 | 60 | 71 | 73 | 3 | 14 | 25 | ||
| 26 | 28 | 39 | 50 | 61 | 72 | 74 | 4 | 15 | ||
| 16 | 27 | 29 | 40 | 51 | 62 | 64 | 75 | 5 | ||
| 6 | 17 | 19 | 30 | 41 | 52 | 63 | 65 | 76 | ||
| 77 | 7 | 18 | 20 | 31 | 42 | 53 | 55 | 66 | ||
| 67 | 78 | 8 | 10 | 21 | 32 | 43 | 54 | 56 | ||
| 57 | 68 | 79 | 9 | 11 | 22 | 33 | 44 | 46 | ||
| 47 | 58 | 69 | 80 | 1 | 12 | 23 | 34 | 45 | ||
Kwadrat magiczny 10 x 10
Poniższy kwadrat zawiera liczby od 1 do 100 a jego suma magiczna wynosi 505.
| 9 | 84 | 88 | 15 | 94 | 5 | 98 | 2 | 100 | 10 | ||
| 6 | 26 | 76 | 77 | 23 | 22 | 80 | 81 | 19 | 95 | ||
| 83 | 67 | 33 | 32 | 70 | 71 | 29 | 28 | 74 | 18 | ||
| 11 | 59 | 41 | 37 | 63 | 62 | 40 | 36 | 66 | 90 | ||
| 87 | 50 | 52 | 56 | 46 | 47 | 53 | 57 | 43 | 14 | ||
| 12 | 58 | 44 | 48 | 54 | 55 | 45 | 49 | 51 | 89 | ||
| 93 | 35 | 60 | 61 | 39 | 38 | 64 | 65 | 42 | 8 | ||
| 16 | 27 | 73 | 69 | 31 | 30 | 72 | 68 | 34 | 85 | ||
| 97 | 82 | 25 | 24 | 78 | 79 | 21 | 20 | 75 | 4 | ||
| 91 | 17 | 13 | 86 | 7 | 96 | 3 | 99 | 1 | 92 | ||
Powyższy kwadrat magiczny 10 x 10 ma interesującą cechę, O niej wspomina Julian Tuwim w swojej książce pt. "Cicer cum caule czyli groch z kapustą. Panopticum i archiwum kultury. Seria II", "Czytelnik", Warszawa 1959, s. 246, następującymi słowami: HIPERMAGICZNE KWADRACISKO, Nawiązując do artykułu o kwadratach "magicznych" (por. seria I, s. 205), nic oczywiście z magią nie mających współnego, bo konstruowanych według ścisłych formuł matematycznych, zamieszczamy jeszcze magiczniejszy, zupełnie szatański kwadrat. Suma liczb w kratkach pionowych i poziomych, jak również na obu przekatnych daje 505. W mniejszych zaś wewnetrznych kwadratach nowy cud: postępując jak powyżej, otrzymamy w pierwszym kwadracie liczbę 404, w drugim —303 (z wyjątkiem wierszy poziomych J. H.), a w trzecim —202. w jego strukturze można wyodrębnić dwa inne, pełne kwadraty magiczne oraz jeden ułomny kwadrat, co pokazano na poniższej planszy. Sumy liczb w wierszach, kolumnach i na przekątnych poszczególnych kwadratów zaznaczono różnymi kolorami tła. Sumy liczb na przekątnych zawiarają skrajne komórki w prawym dolnym rogu planszy.
Suma magiczna składowego kwadratu 8 x 8 wynosi 404, a kwadratu 4 x 4 - 202. Ułomność kwadratu 6 x 6 polega na tym, że choć sumy liczb w kolumnach i na przekątnych są takie same i równe 303, to sumy liczb w wierszach są różne. Te ostatnie posiadają taką własność, że średnia wartość sum liczb w parach wierszy jest taka sama i równa 303: (263 + 343)/2 = (279 + 327)/2 = (311 + 295)/2 = 303.
| 9 | 84 | 88 | 15 | 94 | 5 | 98 | 2 | 100 | 10 | ||||
| 6 | 26 | 76 | 77 | 23 | 22 | 80 | 81 | 19 | 95 | ||||
| 83 | 67 | 33 | 32 | 70 | 71 | 29 | 28 | 74 | 18 | ||||
| 11 | 59 | 41 | 37 | 63 | 62 | 40 | 36 | 66 | 90 | ||||
| 87 | 50 | 52 | 56 | 46 | 47 | 53 | 57 | 43 | 14 | ||||
| 12 | 58 | 44 | 48 | 54 | 55 | 45 | 49 | 51 | 89 | ||||
| 93 | 35 | 60 | 61 | 39 | 38 | 64 | 65 | 42 | 8 | ||||
| 16 | 27 | 73 | 69 | 31 | 30 | 72 | 68 | 34 | 85 | ||||
| 97 | 82 | 25 | 24 | 78 | 79 | 21 | 20 | 75 | 4 | ||||
| 91 | 17 | 13 | 86 | 7 | 96 | 3 | 99 | 1 | 92 | ||||