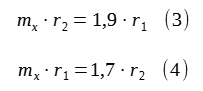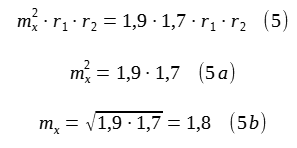Rozrywki matematyczne i nie tylko
Matematyka jest to królowa wszystkich nauk, jej ulubieńcem jest prawda, a prostość i oczywistość jej strojem... Matematyka, która tyle zrobiła przysług towarzystwu, naukom i sztukom, stanie się jeszcze wodzem
ludzkiego umysłu we wszystkich poznawaniach.
{Jan Śniadecki, 1756-1830}
Matematyka jest piękną dziedziną nauki. Nie ma w niej miejsca na ideologię, jak np. w naukach humanistycznych i społecznych. Wyniki i sukces można osiągnąć dzięki wysiłkowi intelektualnemu — rzetelnej wiedzy, logicznemu myśleniu i niekonwencjonalnej wyobraźni. Zajmowanie się matematyką nie musi być tylko pracą, może być też przygodą intelektualną, ale i formą rozrywki związanej z gimnastyką umysłową - łamigłówkami.
Zadanie liczbowe 661
Plansza tego zadania składa się z sześciu wierszy. Wiersze od 1 do 5 zawierają liczby, z których tylko niektóre są widoczne. W drugiej skrajnej kolumnie po prawej stronie pokazane są sumy Si iloczynów zawartości kratek w wierszach:
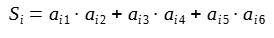 (1)
(1)
Liczby w kratkach tej kolumny mogą zmieniać się w zależności od liczb wpisywanych do pustych kratek danego wiersza. W prawej, skrajnej kolumnie podane są ustalone wartości sumy Si.
| a11 | a12 | a13 | a14 | a15 | a16 | S1 | 160 |
| a21 | a22 | a23 | a24 | a25 | a26 | S2 | 170 |
| a31 | a32 | a33 | a34 | a35 | a36 | S3 | 170 |
| a41 | a42 | a43 | a44 | a45 | a46 | S4 | 140 |
| a51 | a52 | a53 | a54 | a55 | a56 | S5 | 80 |
| a61 | a62 | a63 | a64 | a65 | a66 | S6 | 102 |
Zadanie to polega na wpisaniu liczb napierw do pustych kratek wierszy od 1 do 5 w taki sposób, aby sumy Si w przedostatniej kolumnie po prawej stronie były równe wartościom w ostatniej kolumnie. Po zrobieniu tego i uważnemu przyjrzeniu się otrzymanemu obrazowi planszy, należy uzupełnić odpowiednimi liczbami puste kratki ostatniego wiersza.
| 1 | 50 | 2 | 25 | 3 | 20 | 160 | |
| 2 | 25 | 3 | 20 | 4 | 15 | 170 | |
| 3 | 20 | 4 | 15 | 5 | 10 | 170 | |
| 4 | 15 | 5 | 10 | 6 | 5 | 140 | |
| 5 | 10 | 6 | 5 | 7 | 0 | 80 | |
| 5 | 9 | 102 |
Aby zobaczyć rozwiązanie zadania kliknij → 
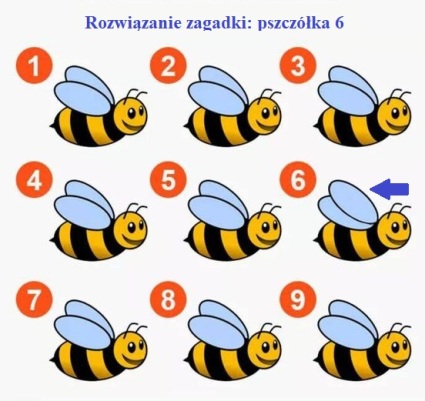
Sprawdzian spostrzegawczości
Inna pszczółka
Różne liczby?
Zrzut skoczka
Zadaniem skoczka jest wylądowanie w kwadracie, którego powiększenie pokazano na rys. 1. Należy znaleźć ten kwadrat na mapie na rys. 2.

Rys. 1. Rejon zrzutu skoczka w powiększeniu.
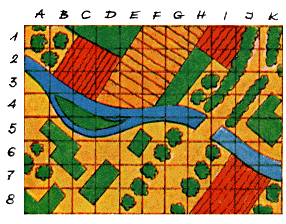
Rys. 2. Mapa z rejonem zrzutu skoczka.
Aby zobaczyć odpowiedź kliknij → 
Liczenie trójkątów
Powiedz, ile trójkatów widzisz na poniższym rysunku.

Aby zobaczyć poprawną odpowiedź kliknij → 
Liczenie żabek
Powiedz, ile zielonych żabek widzisz na poniższym rysunku. Jeżeli chcesz go powiększyć, kliknij na nim.


Aby zobaczyć poprawną odpowiedź kliknij → 
Ważenie — temat ważny dla poważnych
Ważenie było zawsze ważną czynnością. Wagi i odważniki miały swoje miejsce w kuchniach, stały na każdej ladzie sklepowej, można je było zobaczyć w sklepach jubilerskich, aptekach i laboratoriach. Dzisiaj, kiedy kupuje się wyroby porcjowane oraz wstępnie przygotowane i gotowe do spożyciam kuchenne wagi szalkowe spotyka się rzadziej, ale ważenie stanowi nadal wdzięczny przedmiot łamigłówek umysłowych.
Reklamacja
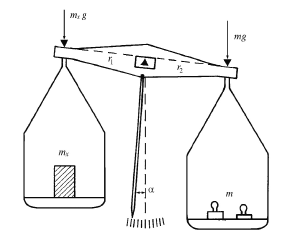
Gospodyni kupiła w sklepie dwie kilogramowe torebki mąki. Po przyjściu do domu zważyła je na swojej kuchennej wadze szalkowej i stwierdziła, że ważą mniej niż 2 kg. Wróciła więc do sklepu i złożyła reklamację. Sprzedawczyni uznała ją
za nieuzasadnioną. Przysłuchujący się sporowi mężczyzna zaproponował powtórne ważenie obydwu torebek. Sprzedawczyni położyła torebki z mąką na lewej szalce, a odważniki na prawej. Wynik ważenia był 1,9 kg. Mężczyzna przełożył torebki
na prawą szalkę, a odważniki położył na lewej. Wynik ważenia był teraz 1,7 kg. Teraz mężczyzna wyjął smartfon i na jego kalkulatorze wykonał jakieś obliczenia i powiedział: W torebkach jest tylko 1,8 kg mąki
.
Czy mężczyzna miał rację?

Aby zobaczyć odpowiedź na to pytanie kliknij →
Fałszywe złote krążki
Są cztery stosy złotych krążków. Każdy stos zawiera 5 krążków. W trzech stosach każdy krążek waży 10 gramów, a w czwartym stosie 9 gramów. W jaki sposób można za pomocą jednego ważenia na wadze szalkowej z użyciem odważników ustalić, który stos zawiera lżejsze krążki?

Aby zobaczyć odpowiedź na to pytanie kliknij →
Fałszywa kostka do gry
Mamy pięć kostek, z których jedna jest fałszywa, cięższa albo lżejsza od pozostałych. Jak można ustalić za pomocą dwóch ważeń na wadze dźwigniowej bez odważników, czy fałszywa kostka jest cięższa czy lżejsza od dobrej kostki?

Aby zobaczyć odpowiedź na to pytanie kliknij →
Dzielenie — po równo czy sprawiedliwie?
Podział tortu
Jak podzielić tort trzema cięciami na osiem równych (jednakowej wielkości) części?

Aby zobaczyć odpowiedź na to pytanie kliknij →