Największy wspólny dzielnik (NWD)
NWD dwóch liczb
Największym wspólnym dzielnikiem [ang. the greatest common divisor (GCD), the greatest common factor (GCF), niem. größter gemeinsamer Teiler (ggT), fr. le plus grand commun diviseur (PGCD)] dwóch liczb całkowitych, większych od zera, jest największa dodatnia liczba całkowita, przez którą każda z tych dwóch liczb dzieli się bez reszty.
Szukanie NWD
Istnieje kilka metod obliczania NWD. Ze względów praktycznych poniżej używa się z algorytmu Euklidesa z wykorzystaniem operatora modulo.
Największy wspólny dzielnik (NWD) liczb: i to
Najmniejsza wspólna wielokrotność (NWW)
NWW dwóch liczb
Najmniejsza wspólna wielokrotność [ang. the least/lowest common multiple (LCM), smallest common multiple (SCM), niem. kleinstes gemeinsames Vielfaches (kgV), fr. le plus petit commun multiple (PPCM)] dwóch liczb całkowitych, większych od zera, jest najmniejsza dodatnia liczba całkowita, podzielna przez każdą z tych dwóch liczb bez reszty.
Szukanie NWW
Istnieją różne metody obliczania NWW. Ze względów praktycznych poniżej używa się algorytmu wykorzystującego NWD.
Najmniejsza wspólna wielokrotność (NWW) liczb: i to
Zastosowania NWD i NWW
Działania na ułamkach
Przy dodawaniu, odejmowaniu i porównywaniu ułamków wykorzystuje się pojęcie najmniejszego wspólnego mianownika (NWM) [ang. the lowest/least common denominator (LCD), the least common multiple of the denominators, niem. kleinster gemeinsamer Nenner (kgN), der Hauptnenner, fr. le plus petit commun multiple (PPCM)]. Do znalezienia NWM wykorzystuje się metodę obliczania NWW.
Przykłady
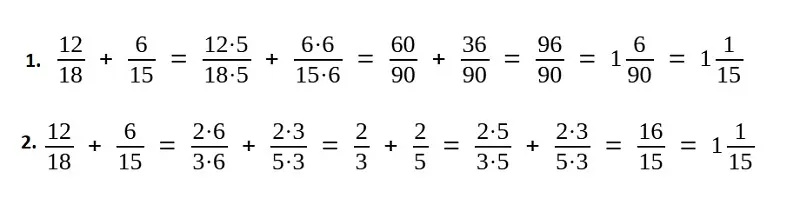
Powyższe przykłady ilustrują dwa sposoby wykonania dodawania ułamków. W pierwszym przykładzie najpierw znajdujemy najmniejszy wspólny mianownik dla mianowników 18 i 15. Dla tych liczb najmniejsza wspólna wielokrotność wynosi 90. Po sprowadzenie obu ułamków do NWM, dodajemy liczniki.W wyniku dodawania otrzymujemy ułamek niewłaściwy (licznik jest większy od mianownika). Po wyciągnięciu całości ułamek właściwy 6/90 sprowadzamy do postaci nieskracalnej 1/15, znajdując największy wspólny dzielnik dla licznika 6 i mianownika 90, którym jest liczba 6.
W drugim przykładzie najpierw sprowadzamy ułamki właściwe do postaci nieskracalnej, znajdując największy wspólny dzielnik dla pierwszego ułamka licznik 12 i mianownik 18, którym jest liczba 6, i drugiego ułamka licznik 6 i mianownik 15, którym jest liczba 3. Następnie znajdujemy najmniejszy wspólny mianownik dla mianowników 3 i 5, którym jest liczba 15, sprowadzemy obydwa ułamki do NWM i po ich rozszerzeniu dodajemy ich liczniki. Z otrzymanego ułamka niewłaściwego wyciągamy całość. Ułamek właściwy 1/15 jest nieskracalny.